So, the fortnightly chunks in the last post were doing ok, but it’s still a bit clunky. I quickly found that the MCMC method I was using couldn’t really cope with shorter intervals (meaning more R values to estimate). So, after a bit of humming and hawing, I dusted off the iterative Ensemble Kalman Filter method that we developed 15 years ago for parameter estimation in climate models I must put a copy up on our web site, it looks like there’s a free version here. For those who are interested in the method, the equations are basically the same as in the standard EnKF used in all sorts of data assimilation applications, but with a couple of tweaks to make it work for a parameter estimation scenario. It had a few notable successes back in the day, though people always sneered at the level of assumptions that it seemed to rely on (to be fair, I was also surprised myself at how well it worked, but found it hard to argue with the results).
And….rather to my surprise….it works brilliantly! I have a separate R value for each day, a sensible prior on this being Brownian motion (small independent random perturbation each day) apart from a large jump on lockdown day. I’ve got 150 parameters in total and everything is sufficiently close to Gaussian and linear that it worked at the first time of asking with no additional tweaks required. One minor detail in the application is that the likelihood calculation is slightly approximate as the algorithm requires this to be approximated by a (multivariate) Gaussian. No big deal really – I’m working in log space for the number of deaths, so the uncertainty is just a multiplicative factor. It means you can’t do the “proper” Poisson/negative binomial thing for death numbers if you care about that, but the reporting process is so much more noisy that I never cared about that anyway and even if I had, model error swamps that level of detail.
The main thing to tweak is how big a daily step to put into the Brownian motion. My first guess was 0.05 and that worked well enough. 0.2 is horrible, generating hugely noisy time series for R, and 0.01 is probably inadequate. I think 0.03 is probably about ok. It’s vulnerable to large policy changes of course but the changes we have seen so far don’t seem to have had much effect. I haven’t done lots of validation but a few experiments suggest it’s about right.
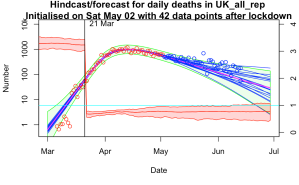
Here are a few examples where (top left) I managed to get a validation failure with a daily step of 0.01 (top right) used 0.2 per day but no explicit lockdown, just to see how it would cope (bottom left) same as top left but with a broader step of 0.03 per day (bottom right) the latest forecast.
I’m feeling a bit smug at how well it’s worked. I’m not sure what other parameter estimation method would work this well, this easily. I’ve had it working with an ensemble of 50, doing 10 iterations = 500 simulations in total though I’ve mostly been using an ensemble of 1000 for 20 iterations just because I can and it’s a bit smoother. That’s for 150 parameters as I mentioned above. The widely-used MCMC method could only do about a dozen parameters and convergence wasn’t perfect with chains of 10000 simulations. I’m sure some statisticians will be able to tell me how I should have been doing it much better…





James,
What time series are you using for the UK? I can go to teh wiki for the UK and those numbers look similar to the JHU time series for the UK. Just curious. TIA
I’m using the official UK numbers straight off gov web site but I do rescale by day of week to remove the weekly cycle. i.e. I work out the average for Mondays, for Tuesdays etc and rescale them to all be the same over the full time series.