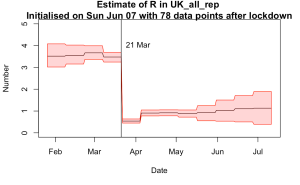
The 2 and now 3-segment piecewise constant approach seems to have worked fairly well but is a bit limited. I’m not really convinced that keeping R fixed for such long period and then allowing a sudden jump is really entirely justifiable, especially now we are talking about a more subtle and piecemeal relaxing of controls.
Ideally I’d like to use a continuous time series of R (eg one value per day), but that would be technically challenging with a naive approach involving a whole lot of parameters to fit. Approaches like epi-estim manage to generate an answer of sorts but that approach is based on a local fit to case numbers, and I don’t trust the case data to be reliable. Also, this approach seems pretty bad when there is a sudden change as at lockdown, with the windowed estimation method generating a slow decline in R instead.
So what I’m trying is a piecewise constant approach, with a chunk length to be determined. I’ll start here with 14 day chunks in which R is held constant, giving us say 12 R values for a 24 week period covering the epidemic (including a bit of a forecast). I choose the starting date to fit the lockdown date at the break between two chunks, giving 4 before and 8 after in this instance.
I’ve got a few choices to make over the prior here, so I’ll show a few different results. The model fit looks ok in all cases so I’m not going to present all of them. This is what we get for the first experiment:

The R values however do depend quite a lot on the details and I’m presenting results from several slightly different approaches in the following 4 plots.
Top left is the simplest version where each chunk has an independent identically distributed prior for R of N(2,12). This is an example of the MCMC algorithm at the point of failure, in fact a little way past that point as the 12 parameters aren’t really very well identified by the data. The results are noisy and unreliable and it hasn’t converged very well. The last few values of R here should just sample the prior as there is no constraint at all on them. That they do such a poor job of that is an indication of what a dodgy sample it is. However it is notable that there is a huge drop in R at the right time when the lockdown is imposed, and the values before and after are roughly in the right ballpark. Not good enough, but enough to be worth pressing on with….
Next plot on top right is when I impose a smoothness constraint. R can still vary from block to block, but deviations between neighbouring values are penalised. The prior is still N(2,12) for each value, so the last values of R trend up towards this range but don’t get there due to smoothness constraint. The result looks much more plausible to me and the MCMC algorithm is performing better too. However, the smoothness constraint shouldn’t apply across the lockdown as there was a large and deliberate change in policy and behaviour at that point.
So the bottom left plot has smoothness constraints applied before and after the lockdown but not across it. Note that the pre-lockdown values are more consistent now and the jump at lockdown date is even more pronounced.
Finally, I don’t really think a prior of N(2,12) is suitable at all times. The last plot uses a prior of N(3,12) before the lockdown and N(1,0.52) after it. This is probably a reasonable representation of what I really think and the algorithm is working nicely.
Here is what it generates in terms of daily death numbers:

There is still a bit of of tweaking to be done but I think this is going to be a better approach than the simple 3-chunk version I’ve been using up to now.






So exponential growth and exponential decay?

So, I still have not joined Curve Plumbing and Pipefitters Anonymous, yet!
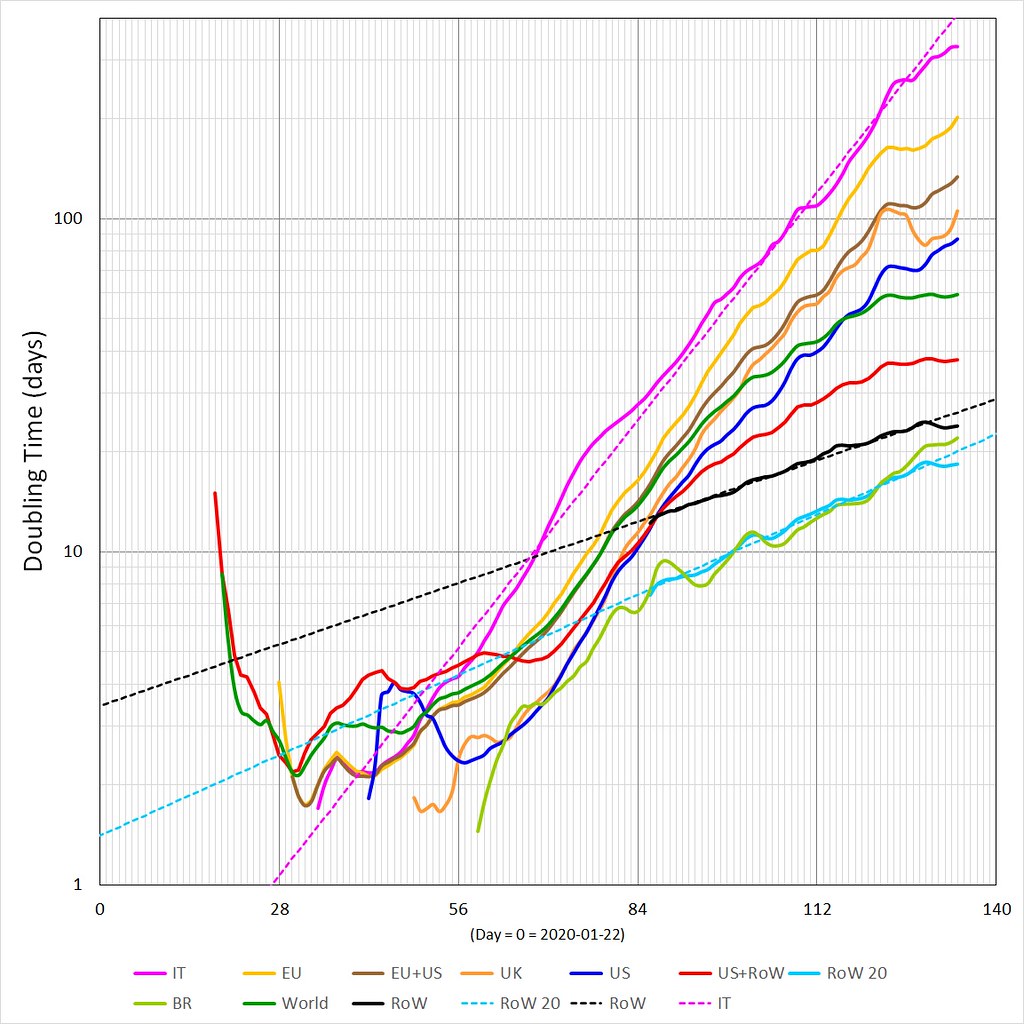
But more to the point, I’m still fixated with doubling time graphs and what does it mean if the various lines have anything in particular to idealized or simplified lines. In this case what does an exponential growth in doubling time mean (e. g. a straight linear line in log-linear space)? And conversely concave up or concave down behaviors, you will notice that of those curves shown above all are currently bending to the RHS).
It turns out that a two parameter Gumbel Max fits the three exponential lines shown (World = WORLD – CN, RoW = WORLD – (CN+EU+US), IT = Italy and RoW 20 = current most active ~20 countries from RoW (I take the statistical moments of daily deaths looking at mostly the m1 (mean in days) and m3 (or skewness))).
The Gumbal Max has an exponential decay but has something else for its growth phase (sort of like a continuous decreasing exponential growth, if you know what I mean, e. g. a distinct concave down behavior from the get go but steepest at its very start in log-linear space).
From all of these doubling time graphs, doubt has creeped in as to the initial behavior, e. g. assuming exponential growth of any significant duration (meaning at least week to ten days or more). The same applies to the decay behaviors when the doubling time series bends to the RHS (e. g. concave down)
I will continue to explore those time series that display less then linear behaviors in log-linear space.
That is all.
All but the last of the four plots shows changes in R occurring in mid June and at he start of July.
How and why?
Just being pulled towards the prior and not constrained by any data. I could certainly change the smoothness constraint and the prior, but I want to represent what I think is happening as fairly as possible. Like I said, a bit of tweaking to do.
Does using Bayesian model selection to determine which change points to include work in problems like this? I don’t know a canonical reference (or much about it anyway beyond existence of the method), but stuff along the lines of these: https://rmgsc.cr.usgs.gov/outgoing/threshold_articles/Perreault2000b.pdf https://www.jstor.org/stable/pdf/2337340.pdf
Why not use a piece-wise linear spline for R, with knots 14 days apart (say) except for two knots close together just before and after the lockdown imposition ??
Yes John it’s a possibility…but piecewise constant is easy and with the inherent smoothing of the model, anything more detailed isn’t necessary. I am also a bit wary of creating artificial extrema that aren’t really supported. Also the model is hard-coded to run with piecewise fixed R so I would have to interpolate (average) back into chunks anyway.
As for the lockdown date…I was originally thinking it would be technically tough to have a discrete choice mixed up with continuous parameters but I’ve eventually managed to realise that the lockdown date can also vary continuously through time anyway, it doesn’t have to be at a day end (doh). So I may have a play with allowing this to vary to see what the model prefers.
Since late April have been plotting ln(d/c) where d is the daily count and c is the cumulative on day n. Because of the low weekend tally I prefer to use a 7 day average for d.
This number falls linearly with time since lockdown. In the uk data there appears to be a change point in early May.
Similar change points can be seen in other countries data for deaths or cases. The change is usually clearer in the case data. Oddly in the UK there is no change in slope for the case data but there is in the death data.
The change appears to correspond to relaxing lockdowns. If this is so then the graph immediately suggests that easing lockdown in the UK has extended the crisis by at least a month, maybe two and will add 7000 to 10,000 deaths. Without more knowledge it is hard to be sure this is the correct interpretation, (perhaps there have been changes in the counting methods, perhaps it is random, just noise). But it is disturbing.
As regards to a change in R I would have expected a change in May that would correspond to the change in ln(d/c).
I think it would be worthwhile to try your model on the ECDC data for other EU countries. In France they locked down, then locked down harder and finally eased up. So there is reason to believe 4 values of R are required for a model as opposed to 2 or 3 for UK data.